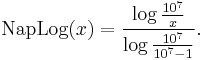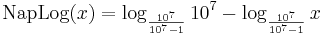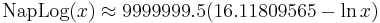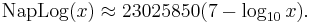Napierian logarithm

The term Napierian logarithm, or Naperian logarithm, is often used to mean the natural logarithm. However, as first defined by John Napier, it is a function given by (in terms of the modern logarithm):

$\mathrm{NapLog}(x) = \frac{\log \frac{10^7}{x}}{\log \frac{10^7}{10^7 - 1}}.$

(Since this is a quotient of logarithms, the base of the logarithm chosen is irrelevant.)

It is not a logarithm to any particular base in the modern sense of the term; however, it can be rewritten as:

$\mathrm{NapLog}(x) = \log_{\frac{10^7}{10^7 - 1}} 10^7 - \log_{\frac{10^7}{10^7 - 1}} x$

and hence it is a linear function of a particular logarithm, and so satisfies identities quite similar to the modern one.

The Napierian logarithm is related to the natural logarithm by the relation

$\mathrm{NapLog} (x) \approx 9999999.5 (16.11809565 - \ln x)$

and to the common logarithm by

$\mathrm{NapLog} (x) \approx 23025850 (7 - \log_{10} x).$

References

Boyer, Carl B.; Merzbach, Uta C. (1991), A History of Mathematics, Wiley, p. 313, ISBN 9780471543978 .
Edwards, Charles Henry (1994), The Historical Development of the Calculus, Springer-Verlag, p. 153 .
Phillips, George McArtney (2000), Two Millennia of Mathematics: from Archimedes to Gauss, CMS Books in Mathematics, 6, Springer-Verlag, p. 61, ISBN 9780387950228 .